Skip to contents

Lotka-Volterra competition model

lotka-volterra-competition.Rmd

The simplest model of interspecific competition included in this package is the two-species Lotka Volterra competition model. In this model, the population growth rate of each species is determined by the density of that species itself, as well as the density of its competitor species. For example, the growth rate of species \(1\) (\(\frac{dN_1}{dt}\)) is determined by the abundance of that species (\(N_1\)), the species’ carrying capacity (\(K_1\)), the density of species 2 (\(N_2\)), and by the relative competitive effect of species \(2\) on species \(1\)):

\[\frac{dN_1}{dt} = r_1N_1\big(1-\frac{N_1 + \alpha N_2}{K_1}\big)\] If the two species are close competitors, then \(\alpha \to 1\), such that the growth of species \(1\) is equally affected by the density of both species.

Similarly, the growth rate of species \(2\) is as follows: \[\frac{dN_2}{dt} = r_2N_2\big(1-\frac{N_2 + \beta N_1}{K_2}\big)\] where \(\beta\) now describes the relative competitive effect of species \(1\) on species \(2\).

We can simulate the dynamics of this model using ecoevoapps using the function run_lvcomp_model() as follows:

library(ecoevoapps)

lvcomp_time <- seq(0, 100, 0.1)
lvcomp_init <- c(N1 = 70, N2 = 50)
lvcomp_params <- c(r1 = .1, r2 = .15, K1 = 500, K2 = 600, a = .5, b = .5)
lvcomp_simulation <- run_lvcomp_model(time = lvcomp_time, init = lvcomp_init, 
                                      params = lvcomp_params)

This generates a dataframe with columns time, N1, and N2:

head(lvcomp_simulation)
#>      time       N1       N2
#> [1,]  0.0 70.00000 50.00000
#> [2,]  0.1 70.56867 50.64733
#> [3,]  0.2 71.14069 51.30183
#> [4,]  0.3 71.71605 51.96357
#> [5,]  0.4 72.29475 52.63258
#> [6,]  0.5 72.87678 53.30893

We can then use the ecoevoapps function plot_lvcomp_time() to generate a trajectory of these populations over time:

plot_lvcomp_time(lvcomp_simulation)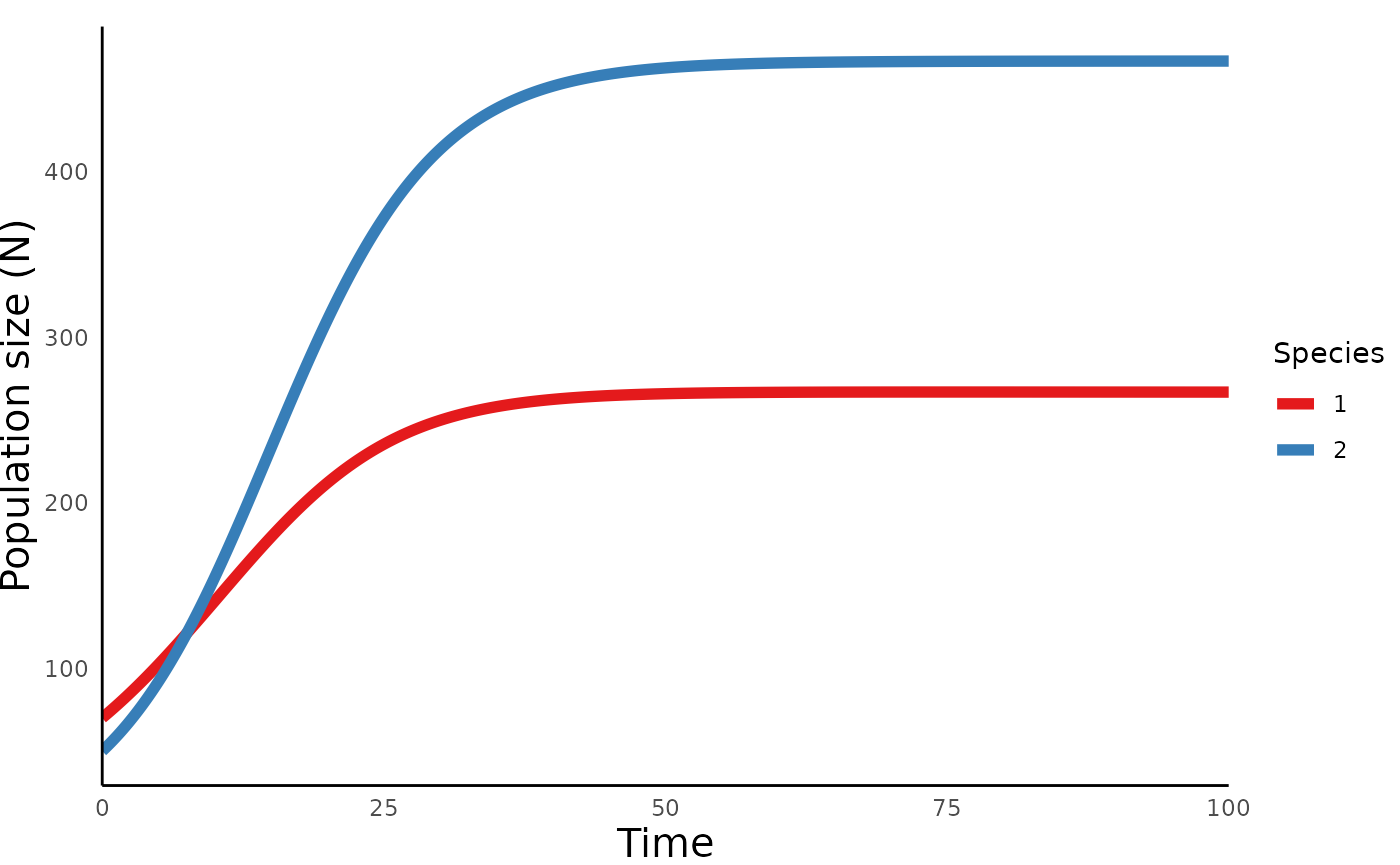

We can also plot the phase portrait of this model, which shows how N1 and N2 change relative to each other over time, using the function plot_lvcomp_portrait(). In this case, we need to provide the function the simulation generated above, as well as the parameter vector we used to generate the simulation. The function uses this information to plot the trajectory of the populations, as well as the “zero net growth isoclines” (ZNGIs). (For more info about ZNGIs, please refer to these resources: link 1, link 2):

plot_lvcomp_portrait(sim_df = lvcomp_simulation, params = lvcomp_params)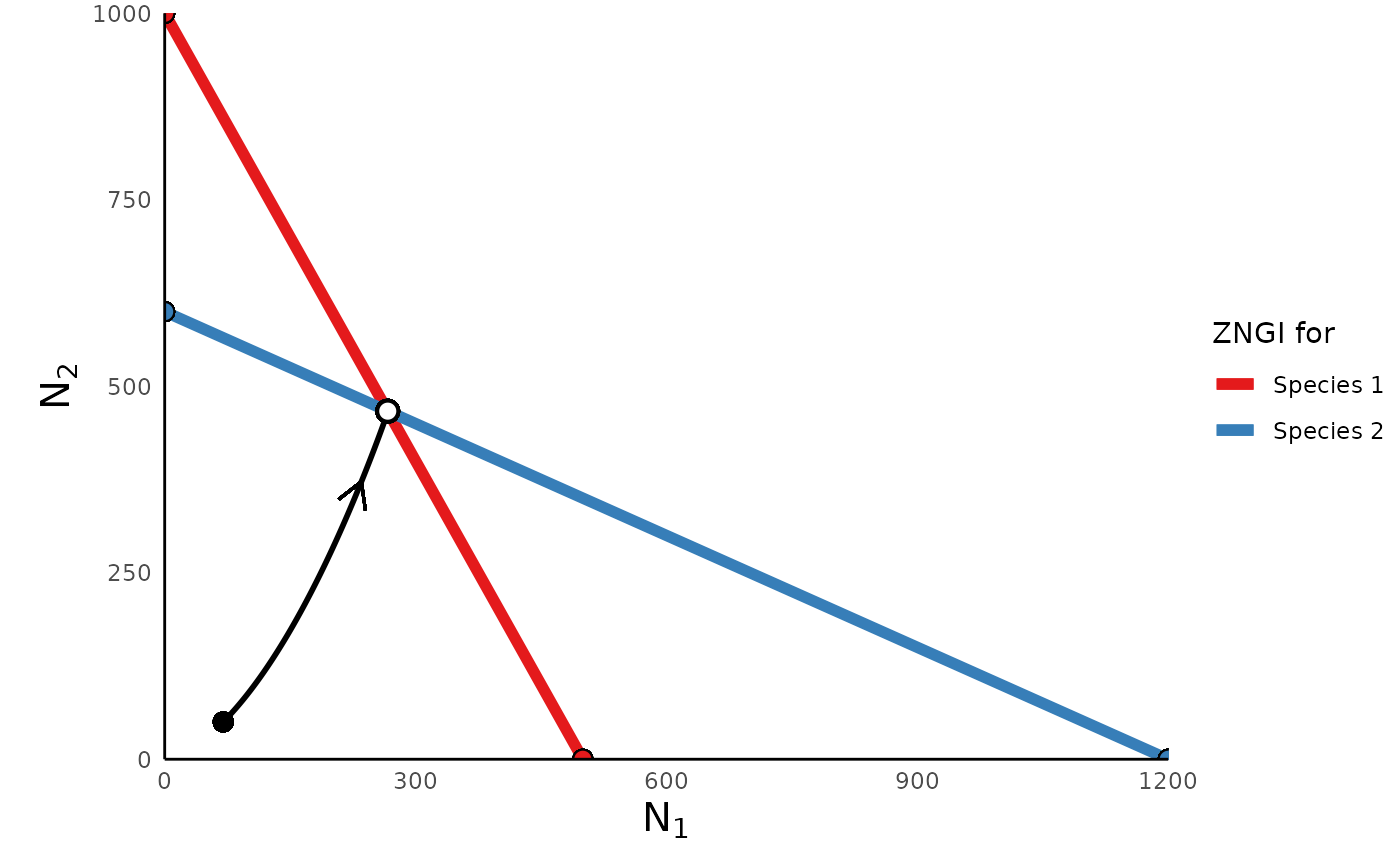

Lotka-Volterra competition in terms of absolute competition coefficients

In the equations above, we expressed the competitive effects of each species on itself (intraspecific competition) in terms of each species’ carrying capacity (\(K_1\) and \(K_2\)), and we described the species’ competitive effects on each other (interspecific competition) in terms of relative competition coefficients (\(\alpha\) and \(\beta\)). We can instead write the Lotka-Volterra competition equation in terms of the absolute effect of intra- and inter-specific competition on each species. Note that in these equations \(\alpha_{ii}\) represents the intraspecific competitive effect in species \(i\), and \(\alpha_{ij}\) describes the effect of species \(j\) on the growth of species \(i\):

\[\frac{dN_1}{dt} = r_1N_1(1-\alpha_{11}N_1 - \alpha_{12}N_2)\] \[\frac{dN_2}{dt} = r_2N_2(1-\alpha_{22}N_2 - \alpha_{21}N_1)\] Note that in this formulation, the carrying capacity of species 1 is simply the inverse of its intraspecific competition coefficient (\(K_1 = 1/{\alpha_{11}}\)), and similarly for species 2 (\(K_2 = 1/{\alpha_{22}}\)).

The run_lvcomp_model() function allows one to define the parameters of Lotka-Volterra competition in this formulation, as shown below:

lvcomp_params_abs <- c(r1 = .5, r2 = .5, 
                       a11 = .002, a22 = .0016, 
                       a12 = .0015, a21 = .001)
lvcomp_simulation_abs <- run_lvcomp_model(time = lvcomp_time, init = lvcomp_init, 
                                          params = lvcomp_params_abs)

plot_lvcomp_time(lvcomp_simulation_abs)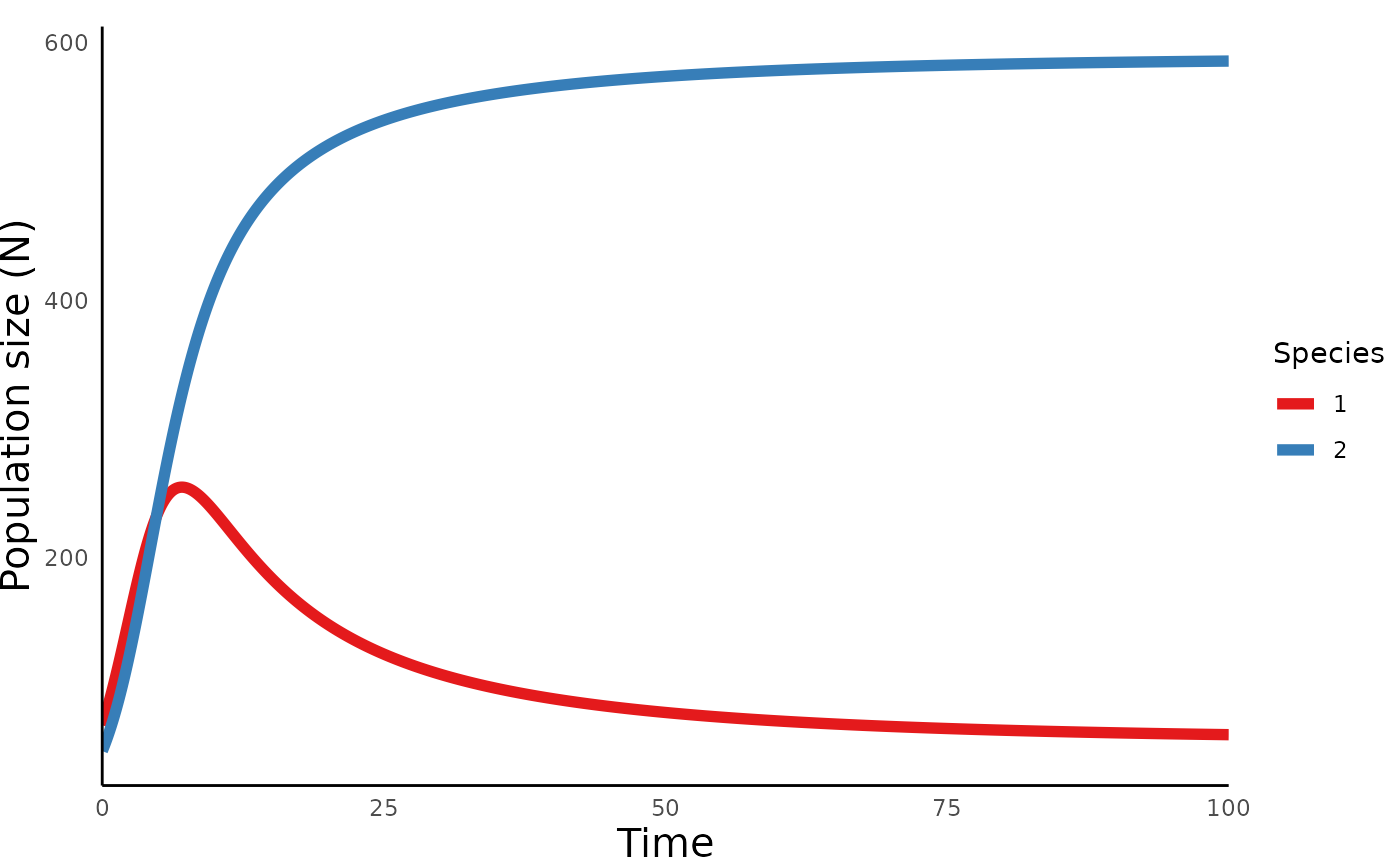

plot_lvcomp_portrait(lvcomp_simulation_abs, lvcomp_params_abs)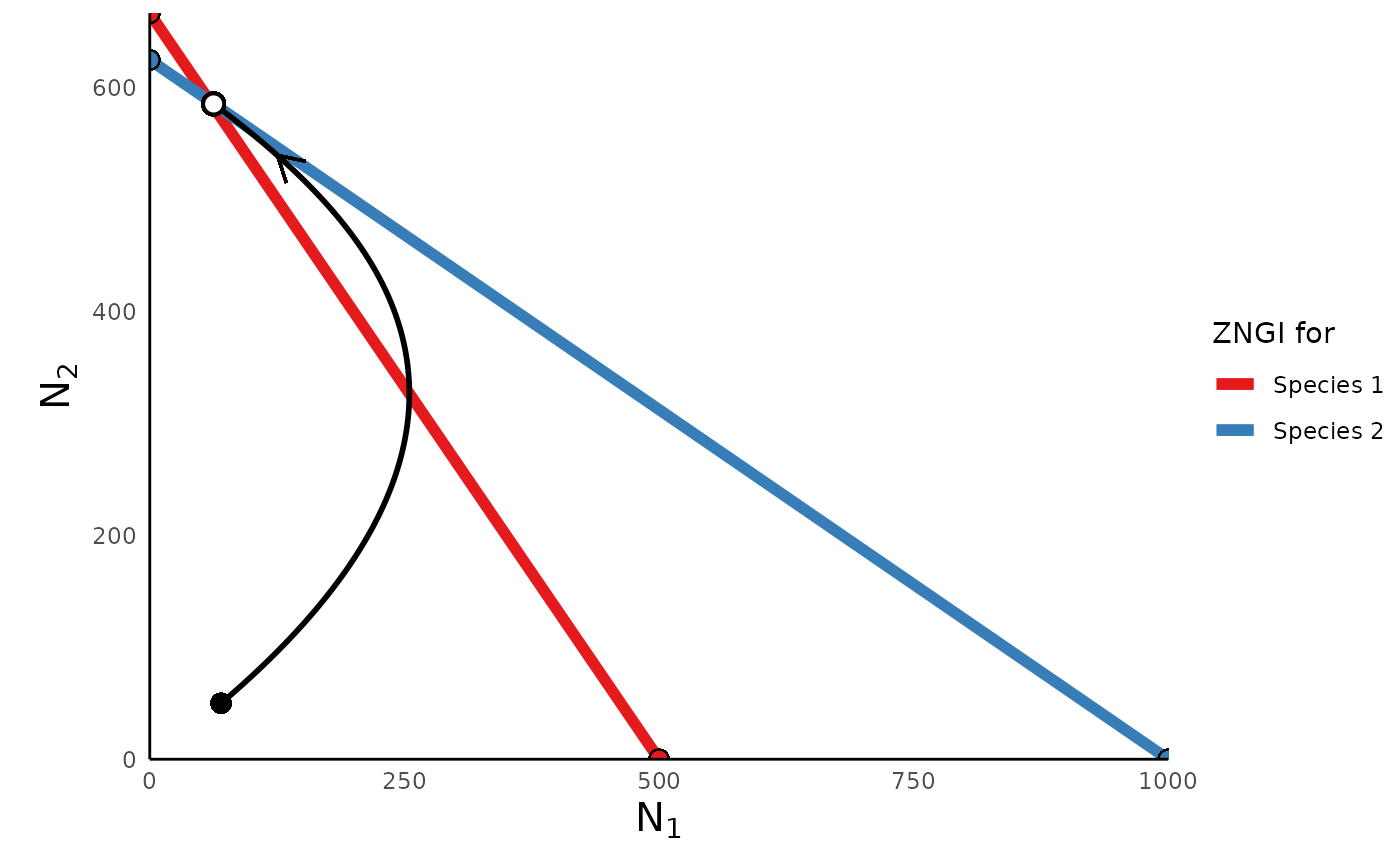

Other References

For more on the Lotka-Volterra competition model, please refer to the following references: